مع انشغال الناس سواءً المختصين في الذكاء الاصطناعي أو غيرهم، بـ ChatGPT، لم يلتفت الكثير من المختصين لمنشور علمي أعتقد أنه عالي الأهمية، بل ربما أعتقد أنه يفوق في أهميته ظهور ChatGPT. إنها الخوارزمية الجديدة Forward-Farward. سأقوم بلفت الانتباه لها هنا، لأنها مجال خصب للبحث الان. ولذلك أنصح الباحثين عن موضوع سيكون له الأثر مستقبلًا، فقد تكون هذه الخوارزمية هي ما تبحث عنه. دعونا نبحر قليلًا مع قصة هذه الخوارزمية الجديدة.
بداية القصة
في عام 1986 قام عالم الذكاء الاصطناعي المشهور Geoffrey Hinton (الأستاذ في جامعة CMU الأمريكية وقتها) بنشر ورقة علمية في مجلة النيتشر Nature مع باحثين آخرين مبتكرين فيها طريقة جديدة للتعلم في النماذج الذكية التي تكون على شكل شبكة مماثلة للخلية العصبية Networks of neurons-like units. هذا الابتكار الجديد الذي تم تسميته Backpropagation ،أو الانتشار العكسي، أحدث نقلة نوعية في مقدرتنا على تدريب الشبكات العصبية التي قامت عليها خوارزميات التعلم العميق Deep Learning Networks.
خوارزمية الانتشار العكسي Backpropagation Algorithm
تقوم فكرة خوارزمية Backpropagation تقوم على أساس أن الشبكة العصبية تقوم بتمرير البيانات من طبقة المدخلات Input Layer الى طبقة المخرجات Output Layer مرورا بالطبقة المخفية Hidden Layer التي يتم فيها استخراج الخصائص وتحديد قيم الأوزان Weights وهذا يسمى Feed Forward Pass. ولكن بعد ان تصل هذه البيانات لطبقة المخرجات يكون هناك Loss Function (دالة الخسارة) التي تقوم بحساب الفارق بين المخرج الذي تنبأت به الشبكة predicted output والمخرج الفعلي actual output. ثم تقوم بتعديل الأوزان بناء على هذا الفارق. والتعديل لايتم بشكل مباشر من الفارق، بل بطريقة غير مباشرة، وذلك بحساب اشتقاق derivative الـ Loss Function. ويكون التعديل باستخدام مقدار التعلم learning rate والتي تمثل معدل قيم التغير في الأوزان في كل مرة يتم التعديل والتي تكون قيمة مختارة بعناية مثل 0.1 او 0.05 وربما أصغر حسب نوع المشكلة وكمية البيانات وحجم الشبكة.
وبشكل أبسط، فإن خوارزمية الانتشار العكسي تقوم بحساب مقدار مساهمة كل عنصر من الـ Parameters في الـ Loss function. وبما أن الشبكة العصبية عبارة عن Graph فيمكن القول أن الانتشار العكسي عبارة عن Chain Rule لهذا الـ Graph. شكرا لـ Chai Rule التي جعلت خوارزمية الانتشار العكسي ممكنة التنفيذ.
وبعد ذلك يتم عمل تعديل لقيم الأوزان والتحيزات بمعدل بسيط في اتجاه الاشتقاق. بهذه الطريقة نضمن أننا نتجه بهذه الأوزان للقيم الأفضل التي تعطيني قيمة خسارة Loss أقل كل مرة.
بهذه الخوارزمية استطعنا أن ندرب شبكات عصبية ذات عمق كبير وأوزان أكثر. وكان نقلة نوعية في عالم الذكاء الاصطناعي. وبالمناسبة هي الطريقة الأكثر استخداما في تدريب الشبكات العصبية اليوم.
الجوانب السلبية في خوارزمية الانتشار العكسي
مع النجاح الكبير الذي حققته هذه الخوارزمية، إلا أن هناك بعض الجوانب السلبية في استخدامها.
وهناك سؤال ملح: هل يستخدم عقل الإنسان طريقة الانتشار العكسي ؟ ينطلق هذا السؤال من حقيقة أن الشبكات العصبية في الالة تحاكي الشبكات العصبية لدى البشر في طريقة العمل.
أغلب الظن أن عقل الإنسان لايرسل موجات عكسية لتحسين اتخاذ القرار. ويكتفي العقل بإرسال الموجات في اتجاه واحد دائما. بغض النظر عن الجهد الكبير الذي يبذل من بعض الباحثين لمحاولة تنفيذ ذلك مع خلايا عصبية حقيقية. ولذلك فنحن في التعلم العميق (الشبكات العصبية العميقة) لانحاكي عقل الإنسان بشكل صحيح.
كما أن المشكلة الأخرى للانتشار العكسي هو تطلبها المعرفة الكاملة بالعمليات التي تمت في مرحلة المرور الأمامي Forward Pass ليتمكن من حساب الاشتقاق. فلو كان هناك جزء من العمليات لايمكننا الاطلاع عليه، فلن نتمكن من حساب الاشتقاق، أي أن عملية الانتشار العكسي لن تكون ممكنة. ولذلك نلجأ لاستخدام Reinforcement Learning في حال كان هناك حالات لايمكن فيها معرفة ما يتم من عمليات. ومع ذلك فهذا الحل يشكو من ارتفاع التباين Variance في لانه يستخدم تعديل قيم الاوزان في كل مرة بشكل عشوائي Random Perturbation. كما انه لايقارن من ناحية الكفاءة مع الانتشار العكسي عندما نتحدق عن شبكات عصبية ذات حجم كبير. ملاحظة: لست هنا بمعرض الحديث عن RL فهو مجال كبير وفيه طرق للتغلب على بعض هذه المشاكل أو على الأقل التخفيف من حدتها.
خوارزمية للأمام للأمام Forward-Forward Algorithm
محاولًا حل سلبيات استخدام خوارزمية الانتشار العكسي، قام Geoffrey Hinton نفسه العام الماضي 2022 وبالتحديد في مؤتمر CVPR الشهير باقتراح طريقة اخرى لا تستخدم الانتشار العكسي الذي اقترحه عام 1986 وسماها خوارزمية للأمام للأمام Forward-Forward Algorithm ولنسمه FF اختصارًا.
تكمن فكرتها باستبدال الفكرة الأولى التي تنطوي على مرورين أحدهما للامام والثاني للخلف، بمرورين ولكن كلاهما للأمام. كلا المرورين سيقومان بنفس العمليات، لكن الفرق بينهما في البيانات المستخدمة في عملية التعلم. حيث ستكون الاولى بيانات صحيحة والأخرى غير صحيحة. يسمى المرور الأول Positive Pass أو المرور الموجب. والثاني يسمى المرور السالب Negative Pass. ستكون مهمة المرور الموجب، استخدام بيانات صحيحة حقيقية لزيادة جودة كل طبقة من طبقات الشبكات العصبية. كما الحال في Forward Pass التعلم العميق الآن. أما المرور السالب، فسيستخدم بيانات غير صحيحة Negative Data، وذلك بتعديل الأوزان في كل طبقة. والفكرة هنا أن البيانات غير الحقيقية يجب أن تقلل جودة النتائج التي تصدر عن الشبكة لتميزها عن البيانات الحقيقية. وهنا ستتعلم الشبكة أن البيانات الحقيقية تعطي نتائج جيدة (ونعني بكلمة جيدة هنا، أي أنها تعطي نتائج فوق قيمة محددة Threshold). بينما البيانات غير الحقيقية تعطي نتائج أقل من تلك القيمة.
تقوم خوارزمية FF المقترحة بعمل Normalization (ربما استطيع ترجمتها بكلمة تسوية أو تنسيب) لقيم الطبقات المخفية قبل ادخالها للطبقة التالية. والسبب لعمل ذلك هو أنه سيكون من السهل في كل طبقة من التفريق بين البيانات الحقيقية والبيانات غير الحقيقية بسهولة لطبيعة عمل دالة جودة البيانات Goodness Function المستخدمة. بمعنى آخر، فإن الطبقة الأولى هي التي ستكون قادرة على التعلم فقط، ولاداعي لاستخراج خصائص جديدة في الطبقات الأخرى. حيث انه من السهل معرفة القيم الكبرى لتكون للبيانات الحقيقية والقيم الصغرى للبيانات غير الحقيقية عن طريق معرفة طول المتجه Vector. أي أن كل طبقة سيكون لها طول جبري معروف (تحدث عن حساب اطوال المتجهات سابقًا) واتجاه. ولكن عمل التسوية سيلغي تأثير الطول ويبقي الاتجاه. وهو الذي سيمرر للطبقة التالية. وهنا ستضطر الطبقة التالية من استخراج خصائص جديدة للبيانات.
تجربة خوارزمية FF
تقدم الورقة العلمية تجارب عدة لهذه الخوارزمية هدفها توضيح أن هذه الخوارزمية تعمل بشكل مقبول على بيانات وشبكات عصبية اصطناعية صغيرة نسبيًّا. وقد استخدم بيانات MNIST الغنية عن التعريف. والهدف من استخدام هذه البيانات الشهيرة، أنها سهلة نسبيا وأن هذه البيانات اشبعت تجربة واي خوارزمية جديدة لن تنجح معها فلن تكون جديرة بالاهتمام ولن نتكلف عناء تجربتها مجددًا. وأما إن نجحت، فنبدأ باثبات جدواها مع بيانات أصعب وأكبر. فيمكن القول أن هذه البيانات هي المرجعية الأولى Benchmark لكل من يدعي أن لديه خوارزمية جديدة.
إذا نظرنا لأداء بعض الخوارزميات الحالية على هذه البيانات سنجد أن شبكة عصبية صغيرة بعدة طبقات مخفية تستخدم خوارزمية الانتشار العكسي تدرب بعدد 20 Epoch، سيكون معدل خطأها قرابة 1.4%.
تحويي بيانات MNIST على آلاف صور خطوط اليد لارقام انجليزية (عربية في رواية أخرى)ـ المهم أنها الأرقام 0،1،2،…،9. ولكن لحاجتنا لاستخدام بيانات غير حقيقية لتدريب شبكة عصبية عميقة تعمل بخوارزمية FF المقترحة. فإن المؤلف قد قام بانشاء بيانات غير حقيقية كما في الشكل ادناه.
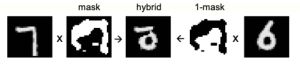
لاحظ أن البيانات الحقيقية هي الرقمين في الطرفين 6 و 7. يتم دمج صورة غيرة حقيقية mask عليها ويتم دمج النواتج لتظهر صورة غير حقيقية هجين من الصورتين Hybrid. هذه الطريقة من انتاج البيانات الخاطئة استخدمها عندما لم يكون هناك تصنيف للبيانات معطى وقت التدريب Unsupervised Learning او التعليم غير الموجه وهي الحالة الأولى للتدريب. أم الحالة الثانية Supervised Learning التعليم الموجه فقد كان يكفي أن يعطي صنف خاطئ للبيانات. فمثلا يدخل له صورة تحوي الرقم 1 بينما الصنف Label التي تدخل معه تكون خاطئة، فتكون مثلًا 8. وقد تم تمرير الصنف Label مع الصورة في اول عشرة خانات Pixels من الصورة، بحيث أن الخانة التي تكون فيها قيمة ال Pixel بيضاء فإنها ترمز للرقم.
وبتدريب النموذج تدريبًا غير موجه باستخدام خوارزمية FF المقترحة، لعدد 100 epochs فإن معدل الخطأ سيكون 1.37%. أما بتدريب النموذج على الحالة الثانية فإن معدل الخطأ بلغ 1.36% بعد 60 Epochs. وهي نتائج مرضية نسبيًا، اذا اخذنا امكانية التطوير على هذه الخوارزمية.
قام الكاتب، بعمل تجارب أخرى كما قام بالتطرق لعلاقة الخوارزمية العتاد Hardware المستخدم وكيف أن هذه الخوارزمية يمكن أن تحررنا من الحاجة للتحويل من ال analog الى digital التي تتطلبها خوارزمية الانتشار العكسي، مما سيقلل استهلاك الطاقة، افترض انا ذلك. كل هذه المعلومات والتفاصيل وأكثر موجودة في الورقة العلمية لمن أراد الاستزادة. https://arxiv.org/abs/2212.13345
نتائج التجارب الأولى خلصت إلى أن الخوارزمية المقترحة FF ابطأ من خوارزمية الانتشار العكسي، كما أنها غيره قابلة للتعميم Not Generalizable في هذه المرحلة. لكن مازال التطوير على الفكرة متاحًا من عدة نواحي، أهمها: أن دالة الجودة Goodness Function المستخدمة كانت Sum of the Square لكل طبقة، والخيارات غيرها كثير. كما أن دالة التفعيل Activation Function المستخدمة هي ReLU ولكن الخيارات غيرها كثير كذلك.
ختامًا، مع أن نتائج هذه الخوارزمية ليست بالاستثنائية في هذه المرحلة مع التقدم الكبير في الشبكات العصبية باستخدام الانتشار العكسي، إلا أنها جديرة بالبحث والتعمق أكثر واكتشاف طرق تحل مشكلاتها الحالية، لفائدتها الكبيرة في التخلص من محاولة إيجاد الاشتقاق لكامل الشبكة والذي يتطلب جهدًا ومعرفة كاملة بما تم على الشبكة خلال المرور الأمامي.

