**كنت أحاول تجنب تحويل هذا الدرس لدرس في الجبر والهندسة لكن مهم جدا أن نستطيع تصور البيانات بالتمثيل الجبري والهندسي لنستطيع التعامل مع البيانات في الكمبيوتر ولذلك سأمر مرور سريع على ما أحاول تجنبه..
كما ذكرنا سابقا، فإن تمثيلنا للبيانات كمصفوفات Matrix والعناصر كمتجهات Vectors ساهم في تعاملنا مع البيانات باستخدام الجبر والهندسة. وحيث تعلمنا في الدرس السابق (مدخل للبيانات: قياس التشابه بين البيانات باستخدام المسافة) كيف نوجد المسافة بين عنصرين وهذا يعطي انطباع عن التشابه بين هذين العنصرين.
في هذا الدرس سنتعلم طريقة أخرى لقياس التشابه بين عنصرين. هذه الطريقة هي بقياس الزاوية بين أي عنصرين. سنقوم باستخدام نفس البيانات من الدرس السابق.
- الزاوية بين عنصرين
الزاوية هندسيا تكون بين خطين متقاطعين. وتكون أصغر زاوية بين هذين الخطين بين درجتي صفر و 180. وإذا أردنا أن نقيس الزاوية بين العنصرين و
والتي سنرمز لها بالرمز
كما في الشكل التالي:
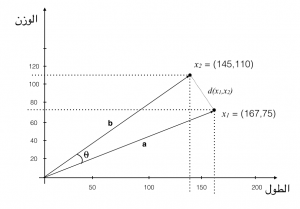
في الحقيقة أننا لانقيس الزاوية بين العنصرين و
. بل إننا نقيسها بين المتجهين
و
الذين يصلان المركز بالنقطتين. ولكن قد نقول أننا نقيس الزاوين بين العنصرين أو المتجهين ونحن نعني الزاوية التي في الشكل السابق.
ولأننا غالبا نميل لتحديد التشابه بين -1 و 1، فإننا لن نستخدم الزاوية لتحديد هذا التشابه بل سنستعيظ عنه بجيب تمام الزاوية Cosine وسنسمي هذه المعادلة لقياس الشبه بين عنصرين بـ Cosine Similarity. قد يتسائل أحدكم لماذا نستخدم جيب التمام Cosine وليس الجيب Sine أو الظل Tangent. الجواب هو لطبيعة حساب جيب التمام. حيث أن حساب جيب التمام Cosine هي حاصل قسمة الضلعين المجاورين للزاوية على بعضهما. أما الجيب والظل فإننا نحتاج للمقابل، وهو في هذه الحالة المسافة بين النقطتين. ونحن هنا لانستفيد من المقابل، بل لانرغب بإدخاله في المعادلة أساساً.
عند حساب جيب التمام Cosine فإننا نحتاج لطول الضلع (في هذه الحالة طول كل من و
). ولكن نحن لانملك طول هذه الأضلاع. وفي الغالب أننا حتى لو امتلكناها فإننا لن نحصل على مثلث قائم الزاوية الذي يتطلبه حساب جيب التمام. وهنا نحتاج أن نتعرف على أمر مهم، وهو التعامد Orthogonality بين المتجهين
و
.
- التعامد Orthogonality
نستطيع أن نقول أن المتجهين و
متعامدين orthogonal إذا كان حاصل ضربهما مساويا لصفر أي:
ولكن ماهي الفائدة أو المعلومة التي يمكن أن نخرج بها إذا عرفنا أن المتجهين متعامدين؟! أترككم تفكرون في الاجابة.
المهم نعود لموضوع الزاوية، إذا كان العنصرين متعامدين فإن الزاوية بينهم ستكون 90 درجة. ماذا نستفيد من هذا؟ سيكون ناتج جيب تمام الزاوية صفر!!! ونعود هنا للبيانات.. فإذا عرفنا أن العنصرين متعامدين هندسيا، فعنده لن يكون هناك تشابه بين العناصر. وإذا كانت الزاوية بينهما صفر درجة، هذا يعني أن العنصرين متشابهين جداً وعنده سيكون جيب التمام يساوي +1. ليس باضرورة أن يكون العنصرين متطابقين تماما ليكونا متشابهين بل يكفي أن يكون أحدهما على خط الآخر وبنفس الاتجاه. والعكس تماما عندما يكونا في اتجاهين مختلفين، كأن يكونا متطابقين مثلاً لكن في اتجاهين مختلفين (أحدهما في الجهة السالبة والآخر في الجهة الموجبة) فإن الزاوية بينهما ستكون 180 درجة وسيكون ناتج جيب التمام للزاوية مساويا لـ -1. أي أن العنصرين متضادين أو مختلفين أو متعاكسين تماما..
ولتلخيص هذه النقاط بشكل واضح، يمكن القول أن التشابه بين العناصر سيكون على ثلاث مستويات:
- أولا، يكون التشابه بينهما موجباً (أي أن الزاوية أصغر من 90 درجة) وهنا يكون التشابه أكبر كلما اقتربت النتيجة Cosine Similarity من العدد +1.
- ثانيا، يكون التشابه بينهما سالباً (أي أن الزاوية أكبر من 90 درجة) وهنا الاختلاف يكون أكبر كلما اقتربت النتيجة من العدد -1.
- ثالثاً، لايكون بينهما تشابه (أي أن الزاوية تكون تساوي 90 درجة) وهنا النتيجة تكون تساوي 0.
يبقى السؤال الأهم هو كيف نحسب جيب تمام الزاوية Cosine Similarity؟!
بقي علينا لنجيب على هذا السؤال هو أن نتعرف على مفهوم جديد هو (متجه ذو وحدة واحدة Unit Vector) **ملاحظة: هذه الترجمة العربية من عندي لأني حاولت أن أجد ترجمة مفهومة فلم أجد..
- متجه ذو وحدة واحدة Unit Vector
المتجه ذو الوحدة الواحدة هو أي متجه يكون طوله واحد any vector with length equals one. وهنا له استخدامات عديدة ليس المجال لها الآن. لكن يمكن تحويل أي متجه لمتجه ذو وحدة واحدة وذلك بقسمة المتجه على طوله. بالطريقة التالية:
ومن هذه الخاصية نستطيع الآن حساب جيب تمام الزاوية وبذلك نحسب التشابه بين العنصرين، كما في المعادلة التالية:
وسيكون ناتج التشابه بحساب جيب تمام الزاوية بين العنصرين x1 و x2 فإن الناتج سيكون كالتالي:
وهذا يعني أن نسبة التشابه بين العنصرين عالية جداً..
قد نطبق في الدرس القادم بإذن الله مع بيانات حقيقية لها أكثر من بعدين مع كتابة الكود الخاص بحساب التشابه بين العناصر حتى نبين كيف نحول الرياضيات لكود وكيف نستفيد من مثل هذه المعلومات.
