في الدرس السابق (مدخل للبيانات: ضرب العناصر وإيجاد أطوالها) تعلمنا كيف نضرب عنصرين وكيف نوجد أطوال العناصر. وفي الحقيقة هذه الخاصيتين لوحدهما قد لاتعطي الانطباع الأفضل في حال تكلمنا عن البيانات. فماذا يعني أن طول عنصر رقم ما؟! وماذا يعني ناتج ضرب عنصرين. فلو قلنا أن العنصرين تمثل معلومات شخصين (في قاعدة بيانات الموظفين أو الطلاب أو المرضى…الخ) فماذا يعني أن طول معلومات الموظف كذا، أو أن ضرب معلومات الموظف الأول في معلومات الموظف الثاني كذا…؟ في الواقع أنها في حد ذاتها قد تكون غير ذات أهمية.. لكن مع ماسنتعلمه اليوم سنجد أن لهاتين الخاصيتين الجبريتين أهمية كبيرة في تحويل هذه البيانات إلى معلومات.
- المسافة بين عنصرين
بما أننا نستطيع أن نمثل البيانات هندسياً، كما رأينا في الدرس الرابع (مدخل للبيانات: التمثيل الهندسي للبيانات) فإن ذلك يعني أن لكل عنصر موقع في الفراغ. وبما أن لكل عنصر موقع فيمكن أن نقيس المسافة بينهما. وبديهياً فإن المسافة بين نقطتين يمكن أن تحسب بعدة طرق، أهمها حساب الفارق بين موقع النقطتين. وهنا، سنعود للمثال الذي استخدمناه في الدرس الرابع. وقد افترضنا أنه لدينا عنصرين إثنين (يمثلان شخصين)، أحدهما والاخر
وكل عنصر لديه خاصيتين، الطول والوزن. (انظر الدرس الرابع لتتذكر ذلك المثال). حيث افترضنا أن العنصر أن العنصر الأول
والعنصر الثاني
والشكل التالي يمثل العنصرين هندسياً:
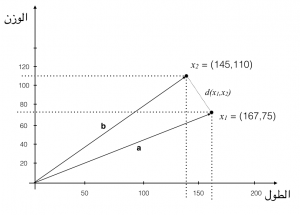
إذا أردنا أن نوجد المسافة بين هذين العنصرين فإننا يمكن أن نقيسها باستخدام المسافة الإكليدية Euclidean Distance. يمكن أن تعود للدرس السابق لتطلع على القاعدة الإكليدية.
كل مانحتاجه هنا هو أن نطرح العنصرين و
ونوجد طول الفرق بينهما باستخدام القاعدة الإكليدية. كما يلي:
تبدو معقدة، أليس كذلك..؟ بل هي أسهل من أن ترعبك. في الواقع من مثالنا الذي نستخدمه هنا، ستكون نتيجة هذه المعادلة كما يلي:
أي أن المسافة بين العنصرين باستخدام Euclidean Distance هي 41.34 ويمكن أن تقاس المسافة بين عناصر مختلفة وإيجاد أكثرها تشابها وذلك بتحديد العناصر التي تكون المسافة بينها أقصر من غيرها. كما أننا اعتبرنا هنا أن عندنا خاصيتين لكل عنصر هي الطول والوزن. لكن الجميل في الموضوع أنه يمكن أن كون عدد الخصائص بالآلاف ولكن ناتج المسافة سيكون عبارة عن رقم واحد. طبق القاعدة السابقة على عنصرين وثلاثة، وزد عدد الخصائص، مثلا أضف خاصية العمر لكل عنصر.
نلاحظ هنا أن العنصرين إذا كانا متطابقين فإن المسافة بينهما ستكون صفراً. كما لايمكن أن تكون المسافة سالبة. ولهذا استخدمنا التربيع ثم أوجدنا الجذر، لنتخلص من الاشارة السالبة.
نكتفي هنا بهذا القدر، وفي الدرس القادم بإذن الله سنتعلم كيف نقيس التشابه باستخدام الزوايا.
