الهندسة تفسر الرياضيات وفروعه المختلفة. إذا تعقدت أمامك معادلة أو مسألة رياضية واستعصى عليك فهمها فمثلها هندسياً وأتوقع أن تسهل عليك كثيراً.
ولذلك رأيت أنه قبل أن ندخل في استخدامات الجبر مع البيانات فإنه من الضروري عرض مثال توضيحي للبيانات هندسياً.
نفرض أن لدينا شخصين طول الأول 167 سم ووزنه 75 كجم. وطول الآخر 145 سم ووزنه 110 كجم. فسيكون شكل البيانات لدينا في مصفوفة ذات بعدين وتحوي عنصرين. كل عنصر يمثل خاصية، فالبعد الأول ويمثل الطول والبعد الثاني
ويمثل الوزن. كما أن كل عنصر يمثل شخص فالعنصر الأول
يمثل الشخص الأول والعنصر الثاني
يمثل الشخص الثاني. وسنمثل هذه البيانات في مصفوفة
كما يلي:
ولتمثيل هذه المصفوفة ذات البعدين هندسياً فإننا نضع لنا بعدين (أو محورين) الأول محور السينات ويمثل الطول والآخر محور الصادات ويمثل الوزن. الشكل التالي يوضح التمثيل الهندسي لهذين العنصرين.
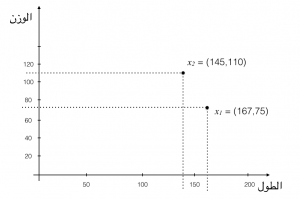
لاحظوا أن تمثيل العنصر عبارة عن نقطة في الفضاء الديكارتي. بينما الخصائص ثمثل بالأبعاد. وبطبيعة العقل البشري فإنه لايستطيع أن يتصور أو يرسم أكثر من ثلاثة أبعاد. ولكن البيانات يمكن أن تحوي عددا كبيراً من الأبعاد وليس بالضرورة أننا نستطيع أن نرسمها أو نتصورها لكي نستطيع أن نطبق أدوات ومعادلات الجبر والتحليل والاحصاء عليها. بل يكفي أن نفهم كيف تتم هذه العمليات على بعدين أو ثلاثة أبعاد لنفهمها على مايتعدى ذلك إلى آلاف بل ملايين الأبعاد.
ولتوضيح توجه العنصر vector. فإننا نرسم لخطا منطلقا من النقطة (0,0) لكل عنصر. ولنسمي التوجه للعنصر الأول a والتوجه للعنصر الثاني b. كما في الشكل التالي.
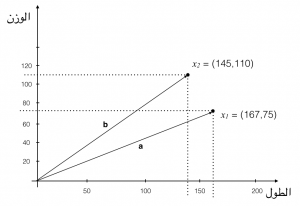
وبوجود a و b يمكن أن نحسب المسافة Distance بين العنصرين x1 و x2. وسنسمي المسافة بينهما d(x1,x2) وتتضح في الشكل التالي:
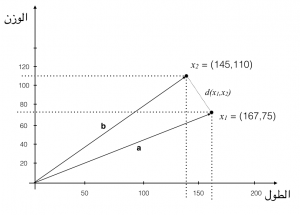
الجميل في الموضوع أننا إذا استطعنا حساب المسافة بين العنصرين قد نستخدم ذلك لتحديد التشابه بين العناصر. فلو كان عندنا ألف شخص، ونريد أن نحسب الشبه بين الأشخاص، فإننا عند إذن سنحسب المسافة بين كل شخصين. ولكن هناك أيضا طريقة أخرى لحساب التشابه بين العناصر، وهو بحساب الزاوين بين الخطين الموجهين a و b. ودعونا نطلق على هذه الزاوية 𝞱.
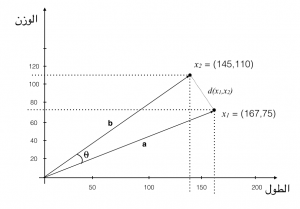
في الدرس القادم بإذن الله سنتعلم كيف نحسب المسافة والزاوية بين هذه العناصر.
