هنا سنتعرف على فائدة الرياضيات وخاصة الجبر والهندسة في علوم البيانات. في الدرس السابق تعلمنا كيف نمثل البيانات هندسياً بشكل بسيط جداً. وسنتعلم هنا كيف نستطيع أن نستفيد من هذا التثميل الهندسي وكذلك الجبري للبيانات في تحويل البيانات إلى معلومات تنبض بالحياة. بحيث سنستطيع أن نقيس وجه الشبه بين عنصرين من عناصر البيانات. فمثلا، لو كان لدينا مجموعة بيانات لمرضى، وأردنا أن نوجد المرضى الذي يتشابهون في الأعراض والحالة الإجتماعية والعمر وخلافه. فإننا سنحدد الخصائص التي نريد قياس التشابه على اساسها ثم نقوم ببعض العمليات الجبرية عليها ليعطينا رقم يحدد الشبه. لكن في مدونة اليوم سنتطرق لعمليتين أو معادلتين أساسيتين في التعامل مع العناصر.
إن تمثيل العناصر على شكل متجه vector أو صف من البيانات وتمثيل كامل البيانات على شكل مصفوفة يساعدنا في إجراء تحليل جبري عليها. وسنفرض أنه لدينا العناصر التالية:
جبرياً، فإن تمثيل هذين العنصرين سيكونان vectors، وهي تمثل جبريا بشكل عمودي. وإذا أردنا أن نمثلها بشكل صف فإننا نحتاج أن نقوم بعملية التبديل Transpose عليها. ويرمز لها جبريا بهذا الشكل: .
ولذلك فإننا في أي عملية جبرية سنعتبر كل عنصر عبارة عن عمود إلا إذا أضفنا حرف T في أعلى الرمز للتبديل.
- حاصل ضرب العناصر Dot Product
نعرف جميعا كيف نضرب عددين لكن كيف نوجد حاصل ضرب العنصرين السابقين؟ ترتيب الخاصائص في كل عنصر ليس عبثياً. بل انها ترمز للشئ نفسه، فمثلا الخاصية الأولى في العنصر i () هي نفس نوع الخاصية الأولى في العنصر j (
) . فمثلا قد يكون الخاصية التي تمثل عمر العنصر(المريض، مثلاً).
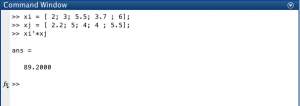
وباستخدام الماتلاب Matlab فقد عرفنا عنصرين وقمنا بعملية الضرب وكانت النتيجة كما في الشكل التالي: (ملاحظة: في الماتلاب نقوب بتبديل العناصر T باستخدام العلاملة (‘)
- طول العنصر، القاعدة الاكليدية Euclidean Norm
نمثل طول العنصر بحساب مجموع خصائصه، وهي أحد العمليات المهمة في الجبر والبيانات على حد سواء وذلك لأن مجموع الخصائص (طول العنصر) قد يعطينا انطباع عن مقدار الخصائص بشكل عام. ونجد أن euclidean norm هي أكثر العمليات استخداما في هذا المجال. ولكن لتجنب القيم السالبة فإننا نربع العدد ثم لنعيد القيم لمقدارها الطبيعي نقوم بجذره تربيعيا. والمعادلة التالية توضح طريقة إجاد طول العنصر باستخدام القاعدة الاكليدية euclidean norm:
إذا كنت أول مرة ترى هذه المعادلة فأرجو أن لا أكون أفزعتك. إنها أسهل مما تبدو عليه رموزها. فإن الرمز في المعادلة ماهو إلا مشابه للقيمة المطلقة في الأعداد التي تعلمناها في المرحلة الابتدائية. والرقم 2 إلى جانب الرمز في الأسفل يمثل مقدار التربيع. ولذلك لو لم نضع هذا الرقم فإن المعادلة ستكون حالة خاصة من القاعدة الاكليدية تسمى L1 norm ، وهي نفسها القيمة المطلقة:
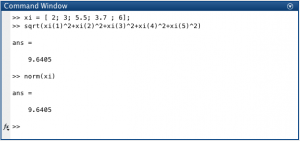
وفي الماتلاب فإن الأمر يبدو أسهل. فلو أردنا أن نقوم بعمل ذلك فإنه يمكن وبسهوله، إما بجمع الخصائص وتربيعها وجذرها أو باستخدام الدالة Method والتي تسمى norm، كما في الشكل التالي:
في المدونة القادمة سنتعلم كيف نستخدم هاتين العمليتين الجبريتين لإيجاد معلومات مهمة عن العناصر بإذن الله.
